大家今天来跟大家伙儿聊聊我最近折腾的一个挺有意思的东西——贝尔不等式。一开始我也是一头雾水,但硬着头皮啃下来之后,发现还挺有成就感的。现在就把我的整个实践过程分享给你们,希望能给同样感兴趣的朋友们一点启发。
缘起:量子力学的“鬼把戏”
事情是这样的,之前我在看一些量子力学的科普文章时,老是看到“量子纠缠”、“贝尔不等式”这些词儿。说是量子纠缠这玩意儿特别神奇,两个粒子不管隔多远,都能瞬间“感应”到对方的状态。爱因斯坦老爷子当年就不信这个邪,觉得这背后肯定有什么咱们不知道的“隐变量”在捣鬼。然后,就蹦出来个贝尔不等式,说能检验这事儿到底有没有“猫腻”。
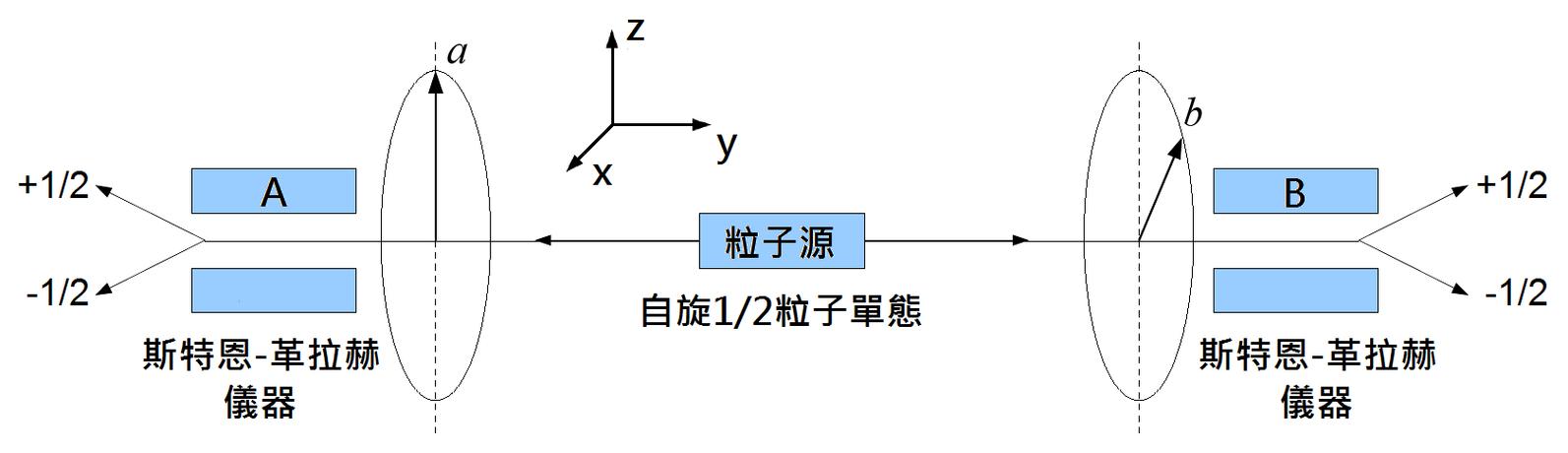
这下可把我好奇心勾起来,心想这贝尔不等式到底是个啥玩意儿?咋还能检验出这么玄乎的东西?于是我就踏上“探秘”贝尔不等式之路。
初探:从一头雾水到“好像懂点”
我找各种资料来看,什么“隐变量理论”、“局域实在性”、“CHSH不等式”……看得我头都大。感觉每个字都认识,但连起来就不知道啥意思。后来我发现好多资料都讲得太“高大上”,动不动就一堆公式,我这数学底子实在有点扛不住。
不过我这人有个“毛病”,就是越搞不懂的东西越想弄明白。于是我就调整策略,找一些相对通俗易懂的资料来看。还真别说,慢慢地,我好像摸到点门道。大概知道贝尔不等式是干啥的,也知道它是怎么来的。
动手:一步步推导贝尔不等式
光看不练假把式!为彻底搞懂贝尔不等式,我决定自己动手推导一遍。这一步,我觉得是最关键的,也是最有收获的。

我找一个相对简单的推导方法,大概是这样的:
- 假设有两个“纠缠”的粒子,它们的状态可以用一些“隐变量”来描述。
- 然后,我们可以对这两个粒子进行不同的测量,测量结果要么是+1,要么是-1。
- 我们根据一些假设,可以推导出一个不等式,这就是贝尔不等式。
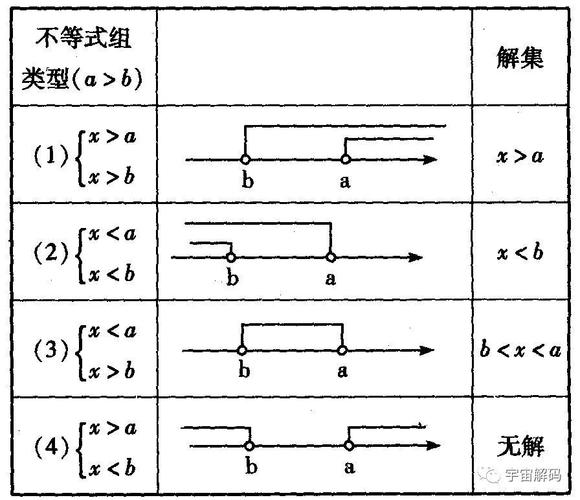
具体的推导过程,我就不在这里详细写,因为涉及到一些数学公式,写出来估计大家看着也头疼。感兴趣的朋友可以自己去网上搜一下,有很多详细的推导教程。
我自己动手推导一遍之后,感觉对贝尔不等式的理解更深一层。以前只是知道它是个“不等式”,现在明白它是怎么一步步推导出来的,以及每一步的含义是什么。
验证:实验才是硬道理
推导出贝尔不等式只是第一步,更重要的是,它能不能经受住实验的检验。毕竟科学这玩意儿,最终还是要靠实验说话的。
我解到,科学家们已经做很多实验来验证贝尔不等式。结果?结果是,实验结果都违反贝尔不等式!也就是说,量子纠缠这事儿,还真就这么“诡异”,爱因斯坦老爷子当年的“隐变量”假设,看来是站不住脚。
看到这里,我心里真是感慨万千。不得不佩服那些科学家的智慧和毅力,能想出这么巧妙的方法来检验量子力学的基本原理。也更加体会到,科学的道路上,充满探索和发现的乐趣。

一点小感悟
折腾完贝尔不等式,我感觉自己对量子力学又多一点点解。虽然还远远谈不上“精通”,但至少不再是“门外汉”。这回经历也让我明白,学习新东西,最重要的就是要有好奇心和耐心。遇到困难不要怕,一点点去啃,总能啃出点名堂来。而且动手实践真的很重要,光看不练,永远也学不透。
今天的分享就到这里。希望我的这点小经验,能对你们有所帮助。咱们下次再聊!
